Modeling Random Walks to Infinity on Primes in Z[√2]
Date:
This work was a spin-off from the paper Walking to Infinity Along Some Number Theory sequences. However, instead of observing sequences of integers which is one-dimensional, we consider primes in the real quadratic integer rings in \(\mathbb{Z}[\sqrt{2}]\), which are of the form \(a+b\sqrt{2}\). This study was inspired by the Gaussian Moat problem posed by Basil Gordon in 1962, and the work has been presented in a couple of conferences by my collegue, Bencheng Li and Daniel Sarnecki.
Abstract
An interesting question known as the Gaussian moat problem asks whether it is possible to walk to infinity on the Gaussian primes with a bounded step size. Our work examine a similar situation in the real quadratic integer ring \(\mathbb{Z}[\sqrt{2}]\) whose primes mostly cluster along the asymptotes \(y = \pm x/\sqrt{2}\) as compared to the Gaussian primes, which congregate only at the origin. We construct a probabilistic model of primes in \(\mathbb{Z}[\sqrt{2}]\) by applying the prime number theorem and a combinatorial theorem for counting the number of lattice points whose absolute values of their norms are no greater than \(n^2\). We then use the model to prove that it is impossible to walk to infinity if the walk remains within some bounded distance from the asymptotes. Lastly, we perform a few moat calculations to show that the longest walk is likely to stay close to the asymptotes; hence, we conjecture that there is no walk to infinity in this case.
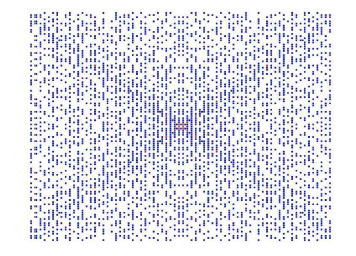
The figure above shows the distribution of primes in the field \(\mathbb{Z}[\sqrt{2}]\).
More Information
This is the link to the pdf of our paper, which is now published on the Journal of Integer Sequences: Modeling Random Walks to Infinity on Primes in \(\mathbb{Z}[\sqrt{2}]\). (With B. Li, S. Miller, D. Sarnecki, T. Popescu) J. Integer Seq. 25 (2022), 21 pp. pdf
This is the link to our paper on ArXiv: Modeling Random Walks to Infinity on Primes in \(\mathbb{Z}[\sqrt{2}]\).
Many Thanks to
I would like to thank Bencheng Li, Daniel Sarnecki, and Tudor Popescu, my collegues, who put a lot of effort into this work, and, most importantly, Professor Steven Miller, who was a really great advisor for this project.
